Formal Languages and Automata

形式语言与自动机

第一章 课程简介与基础知识

课程简介

核心问题：

计算机的基本能力和限制是什么？

1. 究竟哪些问题，可以通过计算解决？——可计算性理论
2. 解决可计算的问题，究竟需要多少资源？——计算复杂性理论
3. 为了研究计算，要使用哪些计算模型？——形式语言与自动机理论

什么是自动机理论？

自动机理论：研究抽象机器机器所能解决问题的理论

• 图灵机
• 有限状态机
• 文法，下推自动机

什么是形式语言？

形式语言：经数学定义的语言

自动机与形式语言的关系

自动机以形式语言为处理对象，形式语言以自动机为形式定义

基础知识

字母表

符号（字符）的非空有穷集

字符串

由字母表中的符号组成的有穷序列

空串

记为 $\epsilon$，有 0 个字符的串

字母表 $\Sigma$ 可以是任意的，但都有 $\epsilon \notin \Sigma$

符号使用的一般约定

• 字母表：大写希腊字母
• 字符：小写拉丁字母 a，b，c 等
• 字符串：小写拉丁字母结尾的几个字母，w，x，y，z 等
• 集合：大写拉丁字母

字符串的长度

字符串中符号所占位置的个数，记为 $|w|$

若字母表为 $\Sigma$，则字符串可递归定义为：

$$|w| = \begin{cases} 0, & w = \epsilon \\ |x| + 1, & w = xa \end{cases}$$

其中 $a$ 是字母表中的字母，$w$ 和 $x$ 是字母表中的字符串

字符串 $x$ 和 $y$​ 的连接

将首尾相接得到新字符串的运算，记为 $xy$，同样，可递归定义为：

$$xy = \begin{cases} x, & y = \epsilon \\ (xz)a, & y=za \end{cases}$$

其中，$a$ 属于字母表，是单个字符，$x, y,z$ 都是字符串

连接运算不满足交换律，但满足结合律

字符串 $x$ 的 $n$ (大于等于0)次幂

递归定义为：

$$x^n=\begin{cases} \epsilon, & n=0 \\ x^{n-1}x, &n >0 \end{cases}$$

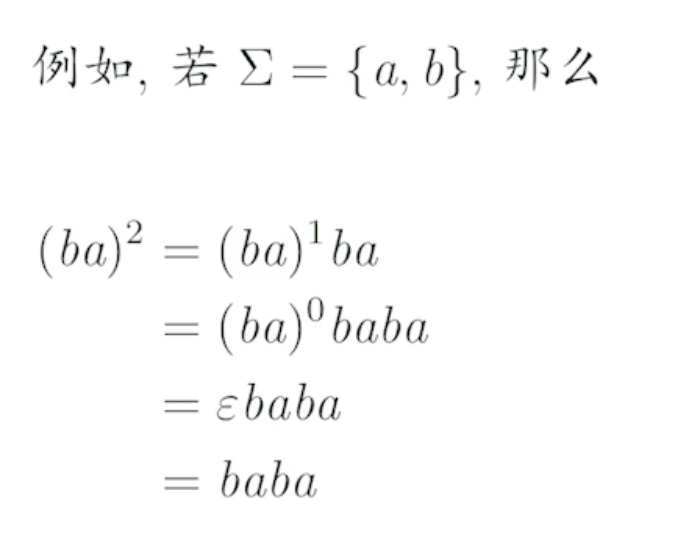
集合的连接

集合 A 和 集合 B 的连接，记为 AB，定义为

$$AB = \{w \mid w=xy,x \in A , y\in B\}$$

集合连接不满足交换律，因为字符串连接不满足交换律

集合的 $n$ 次幂

递归定义为：

$$A^n=\begin{cases} \{\epsilon\}, & n=0\\ A^{n-1}A, &n\ge1 \end{cases}$$

因此，若 $\sum$ 为字母表，则 $\sum^n$ 为 $\sum$ 上长度为 $n$ 的字符串集合，即：

克林闭包

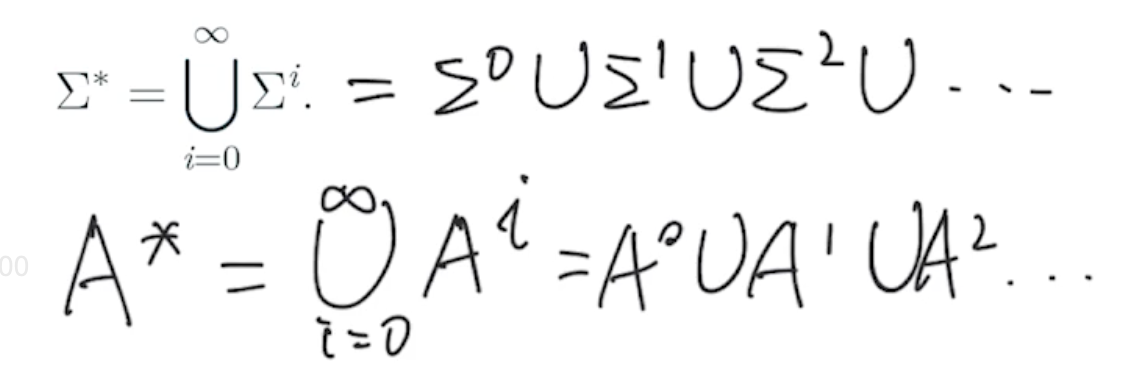
克林闭包是一个字母表或字符串集合其本身的从 0 到 无穷 次幂的并集

正闭包

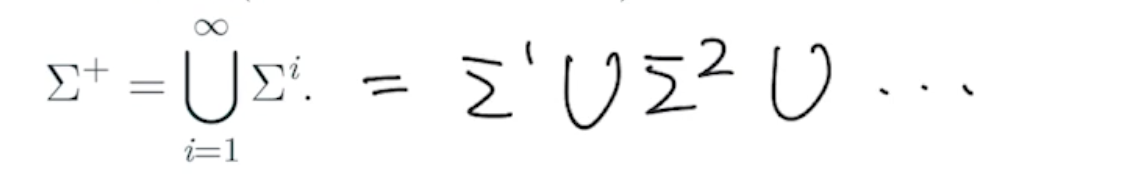
正闭包是一个字母表或字符串集合其本身的从 1 到 无穷 次幂的并集

显然，对于同一个字母表或字符串集合来说，其克林闭包等于其正闭包并上 $\{\epsilon\}$

第二章 有穷自动机

确定的有穷自动机

DFA 的形式定义

有穷状态系统

• 有限状态机：Moore Machine, Mealy Machine

  其现实应用：

  

• 有穷自动机的现实应用

  • 数字电路设计
  • 电脑游戏的 AI 设计
  • 各种通讯协议：TCP、HTTP、Bluetooth、WIFI
  • 文本搜索，词法分析

确定的有穷自动机的构成

• 一条输入带

• 一个读头

• 一个有穷控制器

  

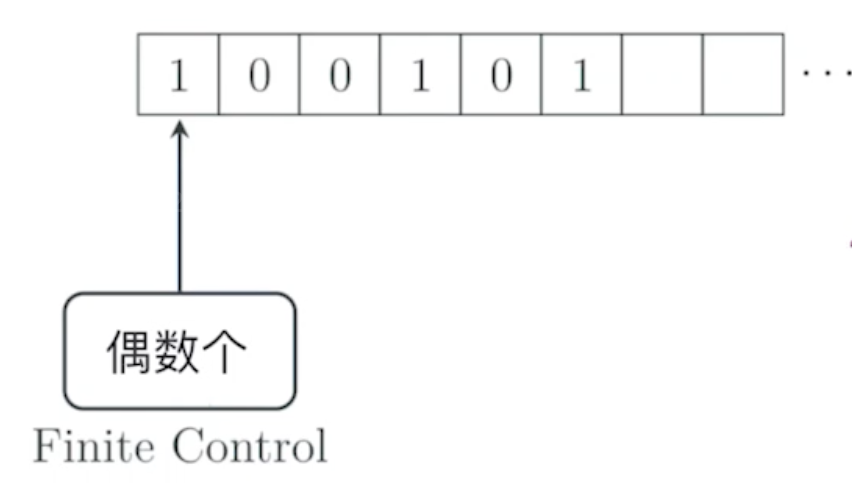
  初始状态非常重要，关系着有穷自动机能否按照预期运行

用形式语言来定义有穷自动机

需要定义如下五个部分：

• 有穷控制器内的几种状态
• 输入带上的字符
• 状态转换规则
• 有穷自动机的初始状态
• 有穷自动机的接受状态

定义：

确定的有穷自动机（DFA，Deterministic Finite Automaton）A 为五元组

$$A=(Q,\Sigma,\delta,q_0,F)$$

• $Q$：有穷状态集
• $\Sigma$：有穷输入符号集或字母表
• $\delta$：状态转移函数，$Q \times \Sigma \rightarrow Q$，即 $\delta(q, a) = p$，当前状态 $q$，输出符号 $a$，状态转换为 $p$
• $q_0$：初始状态
• $F$：终结状态集或接受状态集

例题：

状态转移图和 DFA 设计举例

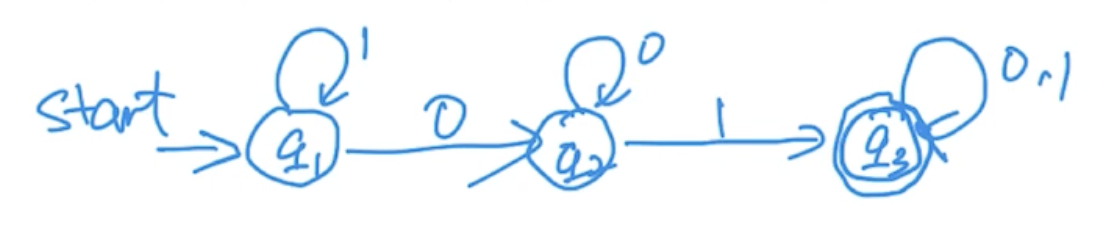
状态转换图

• 每个状态 $q$ 对应一个节点，用圆圈表示
• 状态转移 $\delta(q,a)=p$ 为一条从 $q$ 到 $p$ 且标记为字符 $a$ 的有向边
• 开始状态 $q_0$ 用一个标有 start 的箭头表示
• 接受状态的节点，用双圆圈表示

上述例题的状态转移图如下：

状态转移表

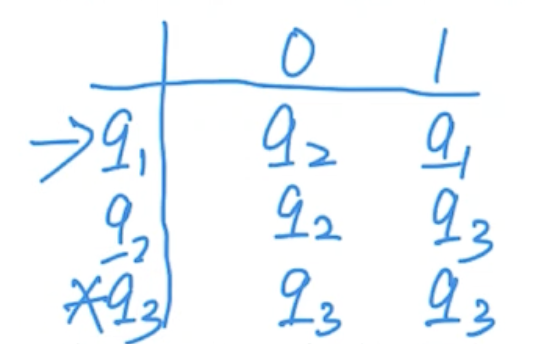
• 每个状态 $q$ 对应一行，每个字符 $a$ 对应一列
• 若有 $\delta(q,a)=p$ ，用第 $q$ 行第 $a$ 列中填入的 $p$ 表示
• 开始状态 $q_0$ 前，标记箭头 $\rightarrow$ 表示
• 接受状态 $q \in F$ 前，标记星号 $*$ 表示

上述列题的状态转移表如下：

几个例题

例题3

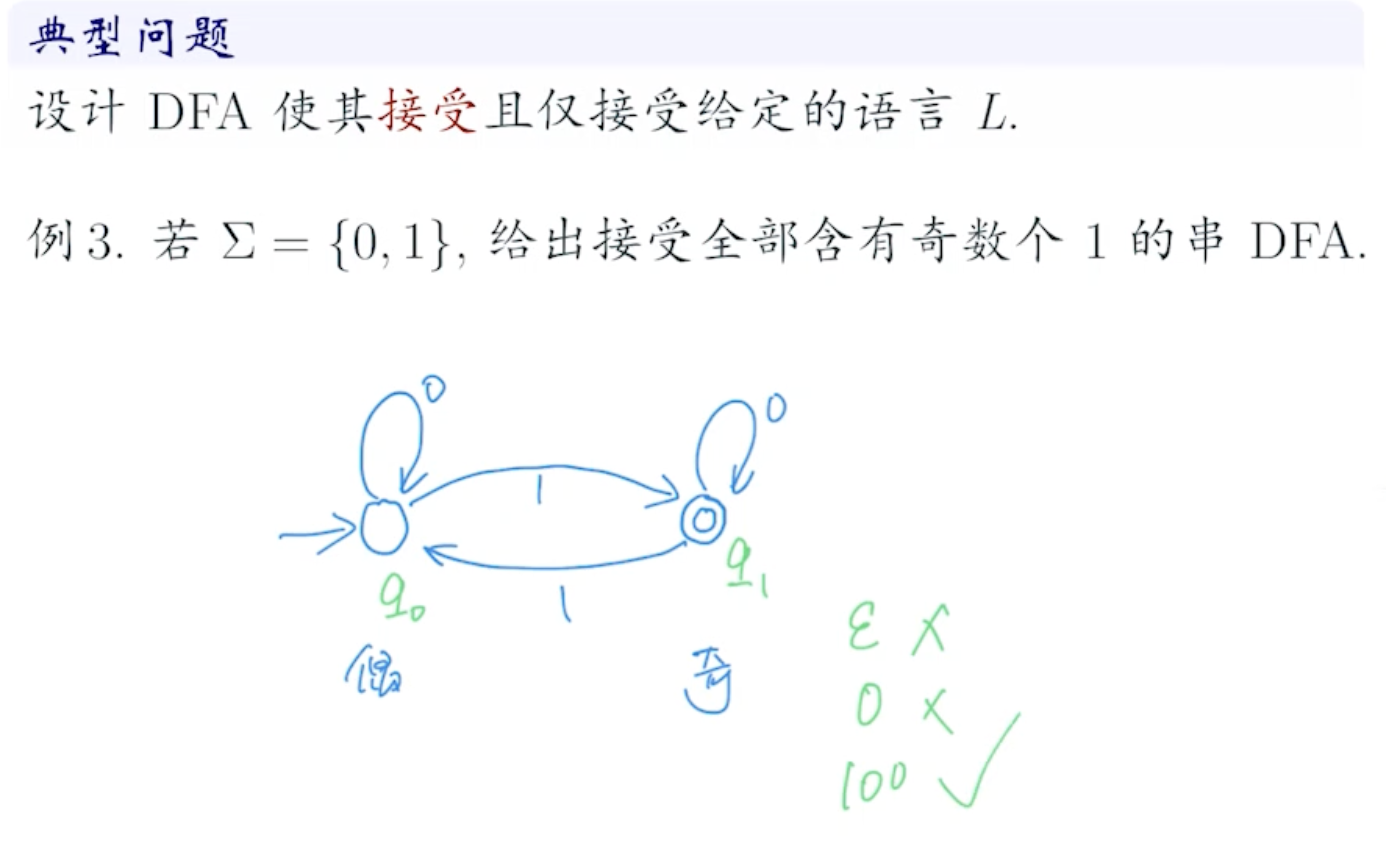
要旨：

1. 分析 $Q$，即有穷状态集中包含哪些状态
2. 分析 $\Sigma$，即看有穷输入符号集中会有哪些符号
3. 确定 $\delta$，分析每个状态在每个符号输入下是如何转换的
4. 确定起始状态 $q_0$ 和接受状态 $F$
5. 画出状态转移图或状态转移表，即设计完毕 DFA
6. 设计完毕后，用几个例子来测试 DFA 的功能是否达到预期

例题4

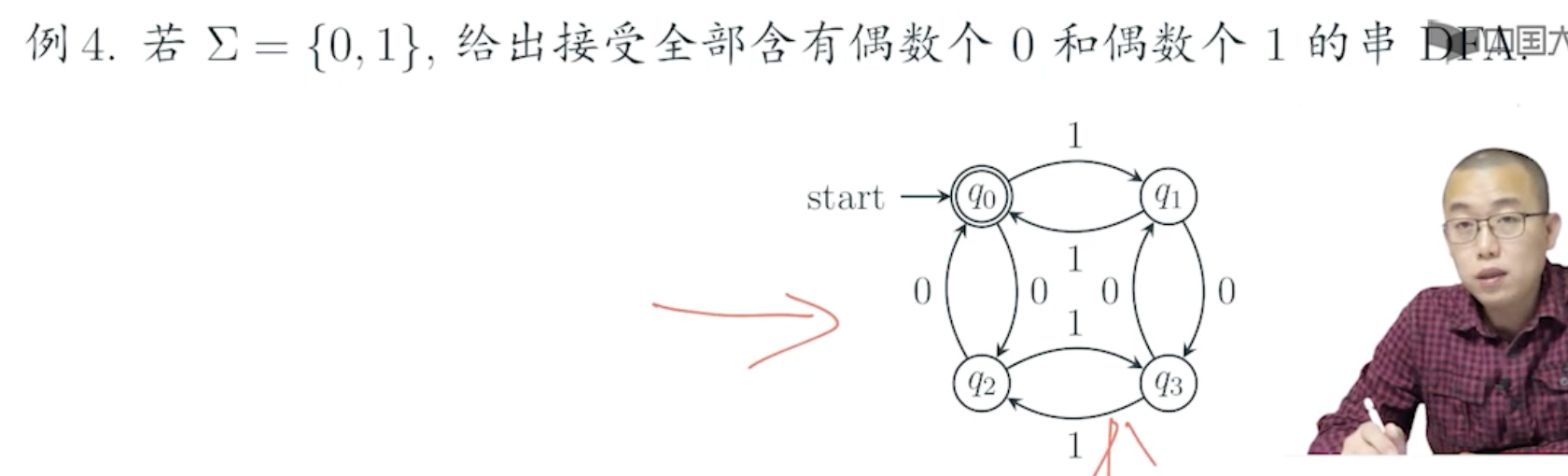
要旨：

与数字逻辑设计类似，首先要判断出一共需要几个状态，其次求每个状态在每个输入下会转换为什么状态，最后画出状态转移图即可

思考题

扩展转移函数和语言

扩展转移函数

由于前面定义的 $\delta$ 只能接收输入字符而不能接收输入字符串，于是我们扩展 $\delta$ 到字符串，定义扩展转移函数： $\hat \delta:Q \times \Sigma^* \rightarrow Q$ 为

$$\hat \delta (q,w) = \begin{cases} q, &w=\epsilon \\ \delta(\hat \delta (q,x),a), & w=xa \end{cases}$$

其中 $a \in \Sigma$, $w,x \in \Sigma^*$

以上是递归的定义，用迭代的思想来说，扩展转移函数就是每次从字符串的开头取一个字符，然后进行状态转移，重复此步骤，直到字符串被取空为止。

技能测试：

1. 不必须，DFA 在任意状态的任意输入下都有结果输出，所以可以从任意状态开始处理字符串。
2. 一定，因为 DFA 的定义保证了它在任意状态接受任意输入都会有输出，所以一定会。

例题：

要旨：

1. 对 y 进行归纳证明
2. $\hat \delta$ 的定义的正用和反用
3. 归纳假设的使用

DFA 的语言与正则语言

DFA 的语言

定义：若 $D = (Q, \Sigma,\delta, q_0,F)$ 是一个 DFA，则 D 接受的语言为

$$L(D) = \{w \in \Sigma^* \mid \hat \delta(q_0\,w) \in F\}$$

即 DFA 的语言是所有经过该 DFA 后得到的输出为该 DFA 的接受状态的字符串的集合。

正则语言

如果语言 $L$ 是某个 DFA D 的语言，即 $L = \bold L(D)$，则称 $L$ 是正则语言

• $\empty ,\{\epsilon\}$ 都是正则语言
• 若 $\Sigma$ 是字母表，则 $\Sigma^*, \Sigma^n$ 都是 $\Sigma$ 上的正则语言

例题：

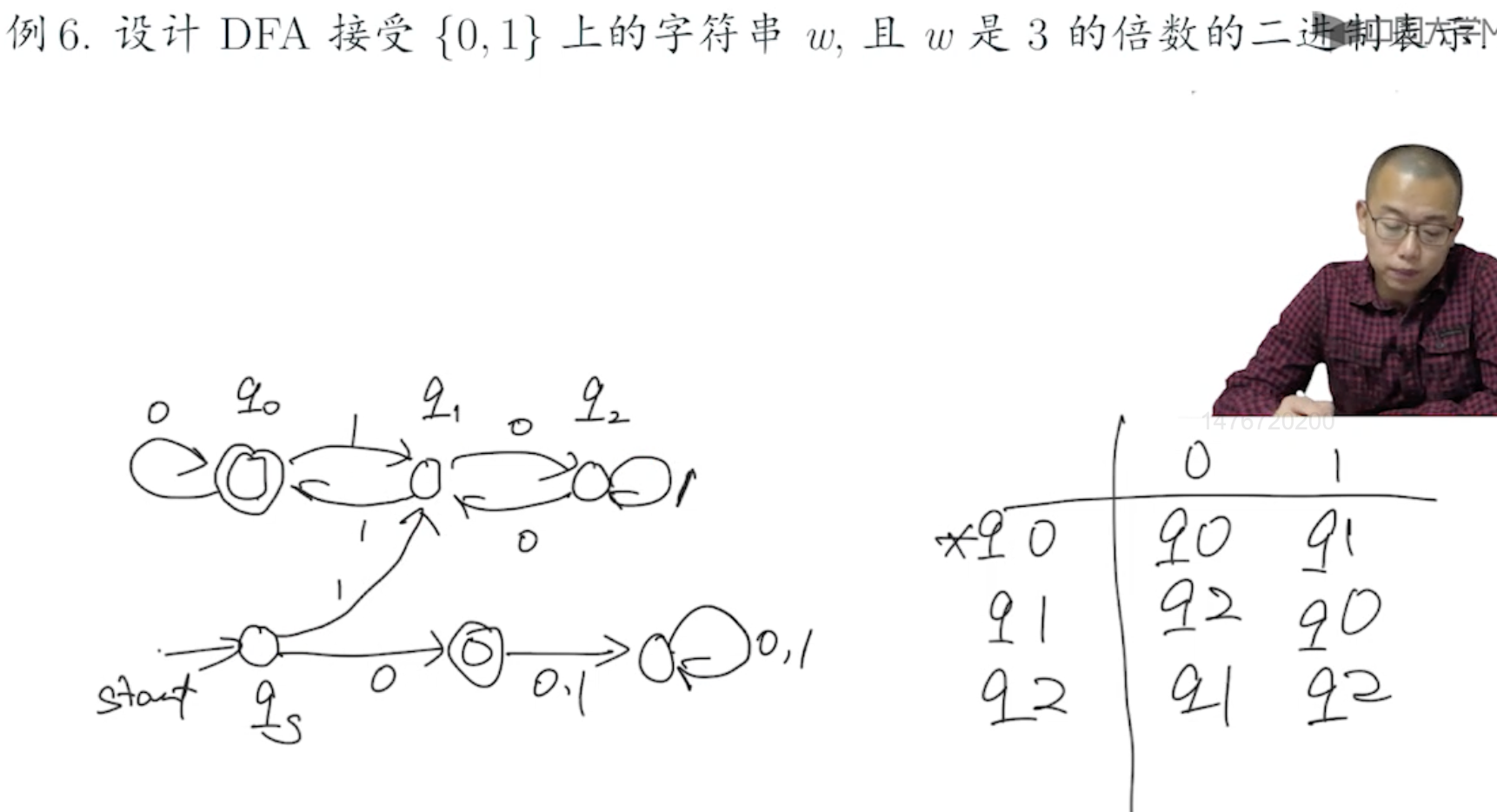
要旨：

1. 设计状态是精髓，考虑到 DFA 无法判断后面到底还有没有字符输入，所以选择的状态要能根据输入动态变化，并通过状态来判定输入是否满足条件
2. 此例题的解答选择的状态是：根据之前的输入所积累的余数为 0/1/2，这样，在每读入一个输入时，就更新当前的余数，即更新当前的状态，余数为 0 则为接受状态
3. 以空串为起始状态，对于以 0 开始的串要特殊处理（以 0 开始的串被认为是非法字符串，不管 0 后面的字符是怎样的，都无法被接受。但如果单只有 0 一个字符，由于 0 可以整除 3，所以接受之）

非确定的有穷自动机

NFA 的形式定义

非确定的有穷自动机指==状态的非确定转移==

• 同一个状态在相同的输入下，可以有多个转移状态
• 自动机可以处在多个当前状态
• 使自动机的设计更容易

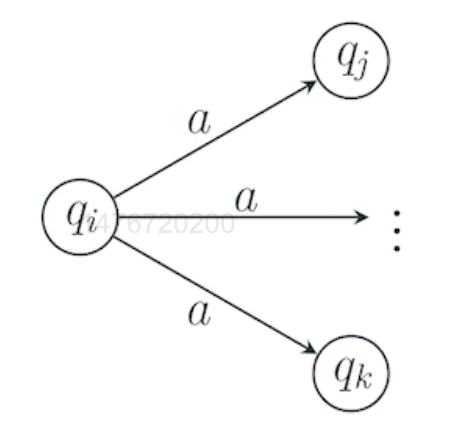
由 DFA 转变到 NFA

思考题：有穷自动机有了非确定性，能否增加它识别语言的能力？

不能。后面会有论述：DFA 和 NFA 是等价的。

非确定的有穷自动机的形式定义

非确定的有穷自动机（NFA， Nondeterministic Finite Automaton）$A$ 为五元组

$$A = (Q, \Sigma,\delta,q_0,F)$$

其中：

• $Q$：有穷状态集
• $\Sigma$：有穷输入符号集或字母表
• $\delta$：$Q \times \Sigma \rightarrow 2^Q$ 状态转移函数（因变量不再是特定状态，而是状态的集合，体现非确定性）
• $q_0 \in Q$：初始状态
• $F \in Q$​：终结状态集或接受状态集

进一步理解

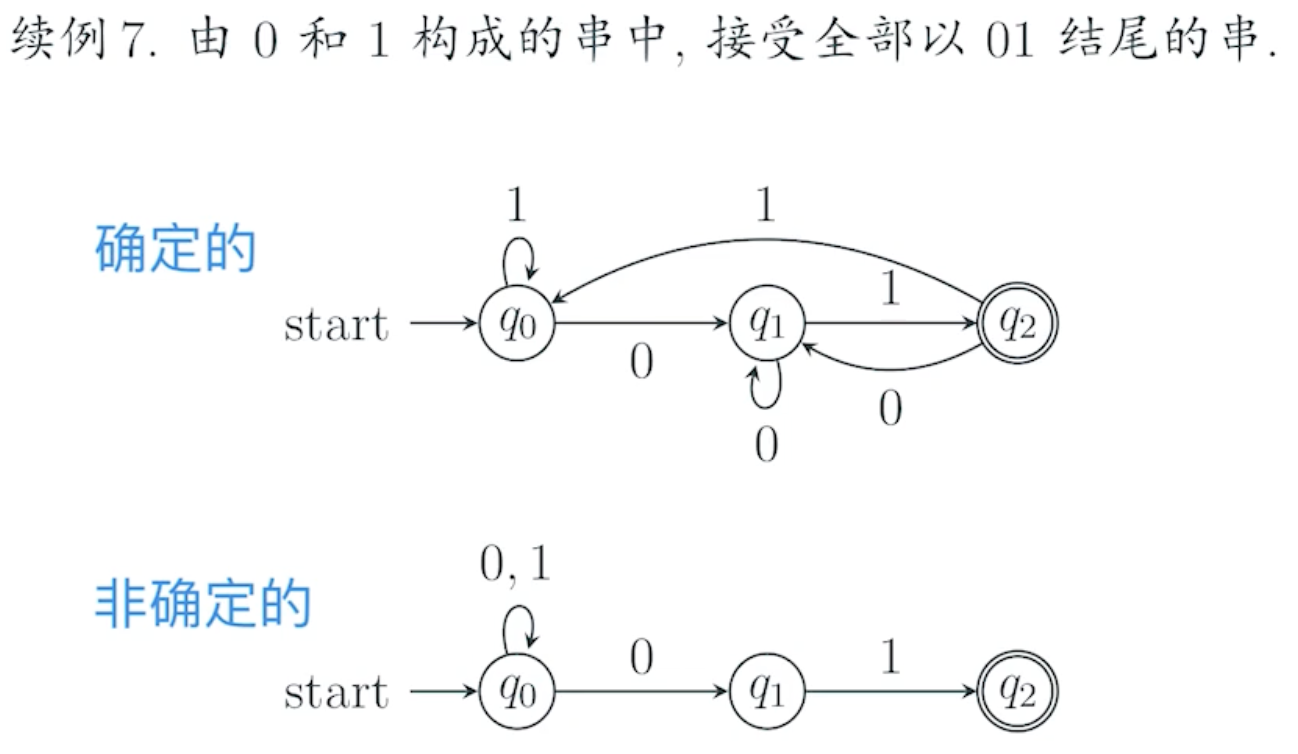
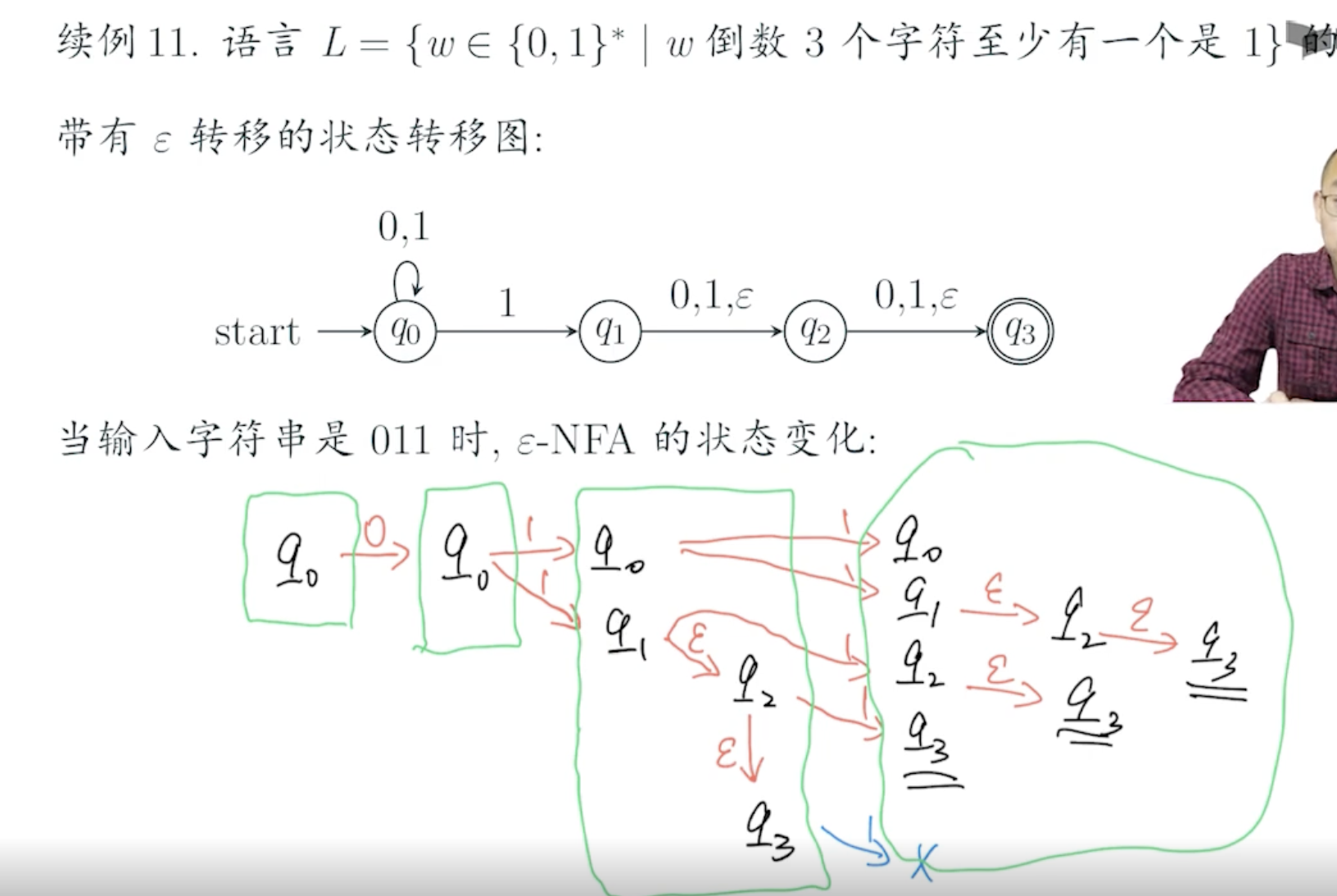
续例7，构造出的 NFA 识别字符串 00101 的过程

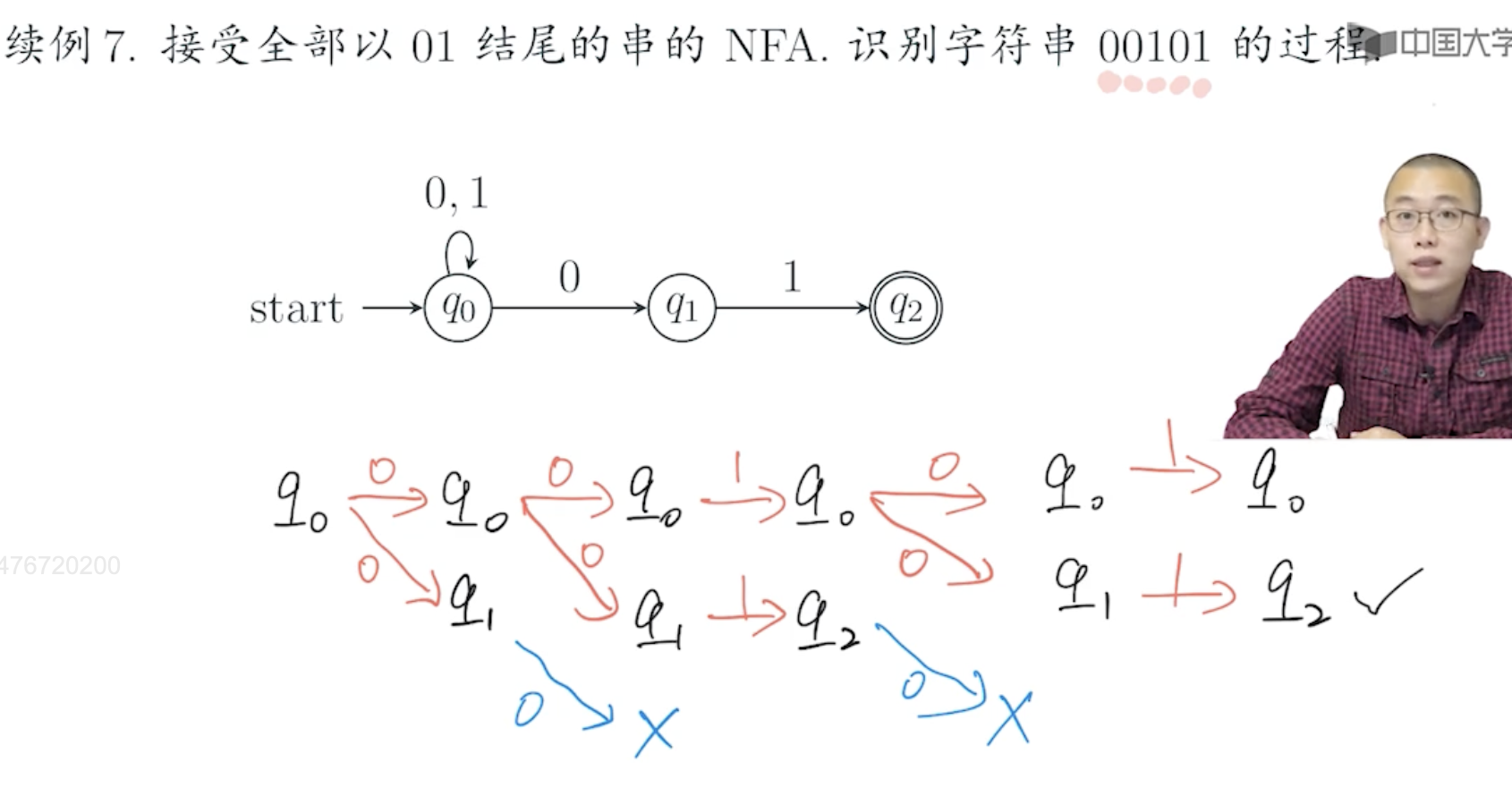
理解：

• 当有多个状态可以跳转时，NFA 就分裂出多个状态来，每个状态都继续往下进行，如果在最后的多个状态中存在接受状态，则认为该字符串是可被接受的。

其状态转移表：

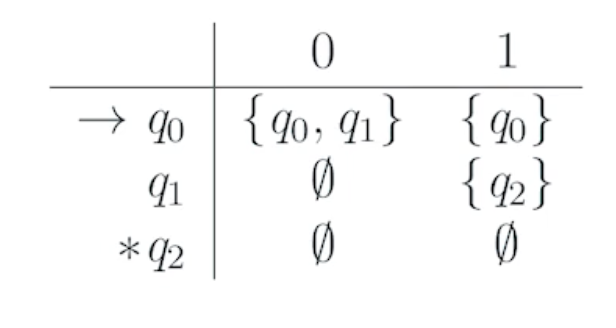
扩展转移函数和语言

扩展转移函数定义

扩展 $\delta$ 到字符串，定义扩展转移函数 $\hat \delta : Q \times \Sigma^* \rightarrow 2^Q$ 为

$$\hat \delta(q,w) = \begin{cases} {q}, & w = \epsilon \\ \bigcup_{p \in \hat \delta(q,x)} \delta(p,a), & w=xa \end{cases}$$

其中 $a \in \Sigma,w,x \in \Sigma^*$

阐释：

• 如果字符串为空串，则状态转移后的状态为原状态（集）
• 如果字符串不是空串，则状态转移后的状态为 $a$ 经过 $\delta$ 转移后的状态集与 $x$ 经过 $\hat \delta$​ 转移后的状态集的并集

NFA 的语言定义

回顾：若 $D = (Q, \Sigma,\delta, q_0,F)$ 是一个 DFA，则 D 接受的语言为

$$\bold L(D) = \{w \in \Sigma^* \mid \hat \delta(q_0\,w) \in F\}$$

若 $N = (Q, \Sigma,\delta,q_0,F)$ 是一个 NFA，则 $N$ 接受的语言为

$$\bold L(N) = \{w \in \Sigma^* \mid \hat \delta(q_0, w) \cap F \neq \empty \}$$

即字符串 $w$ 经过状态转移后的状态集中存在接受状态，则该字符串为 NFA 接受的语言

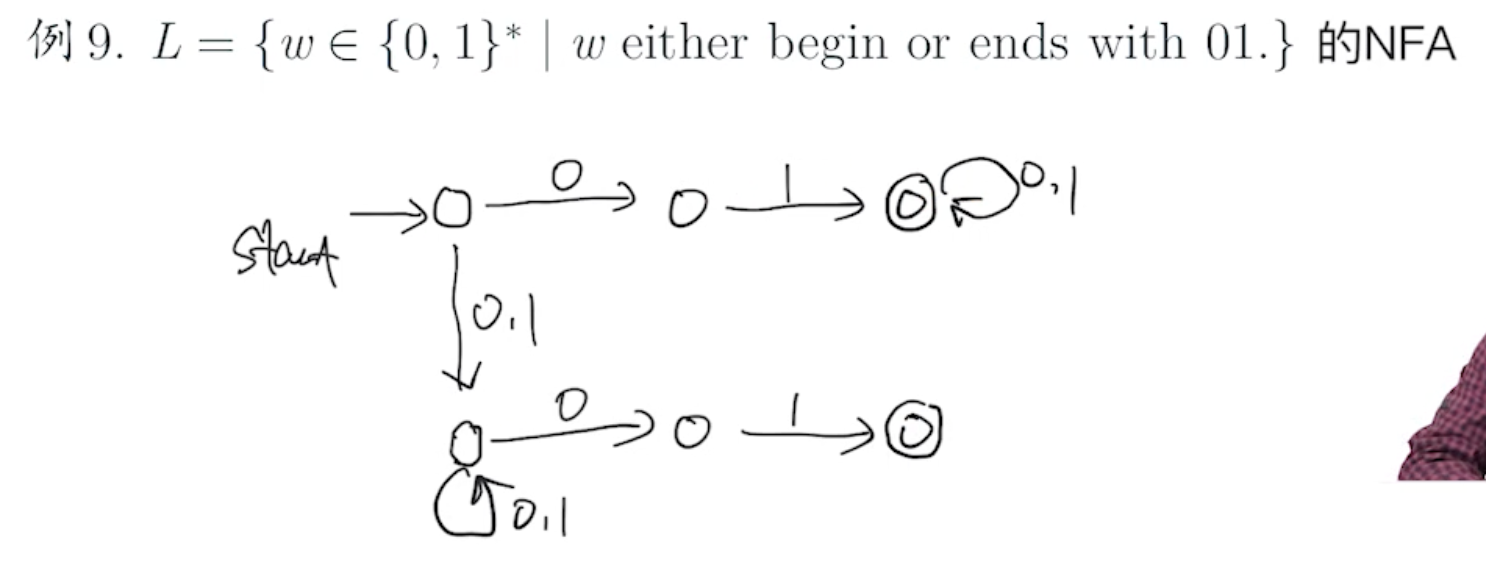
例题9

DFA 与 NFA 的等价性

定理一

如果语言 $L$ 满足被 NFA 接受，当且仅当 $L$ 被 DFA 接受。

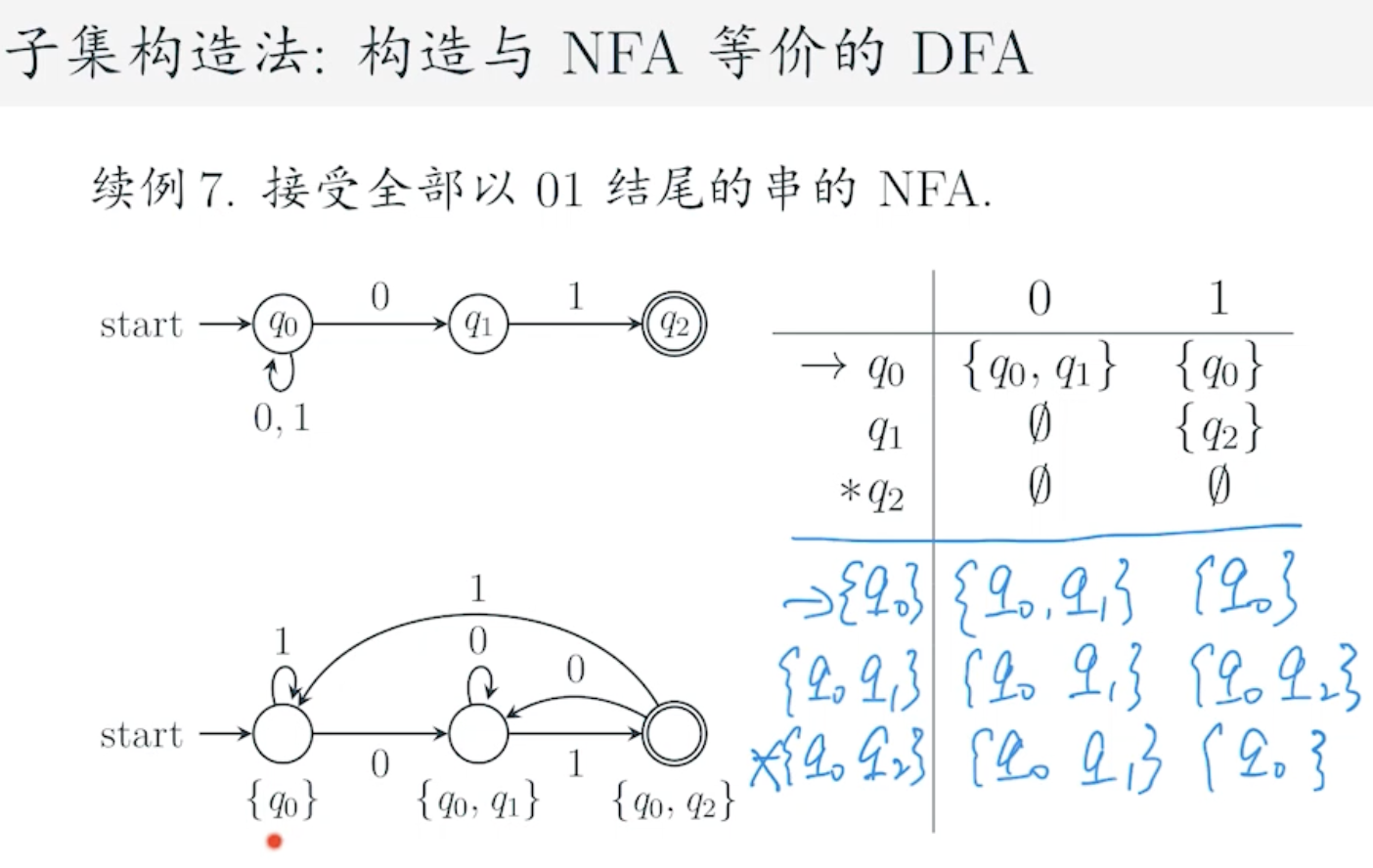
证明方法：==子集构造法==

构造如下：

证明：

例子：用子集构造法来构造与 NFA 等价的 DFA

带有空转移的非确定的有穷自动机

$\epsilon$​-NFA 的形式定义

状态的 $\epsilon$ 转移

• 允许状态因空串 $\epsilon$ 而转移，即不消耗输入字符就发生状态的改变

• 使自动机的设计更容易

• 例子：

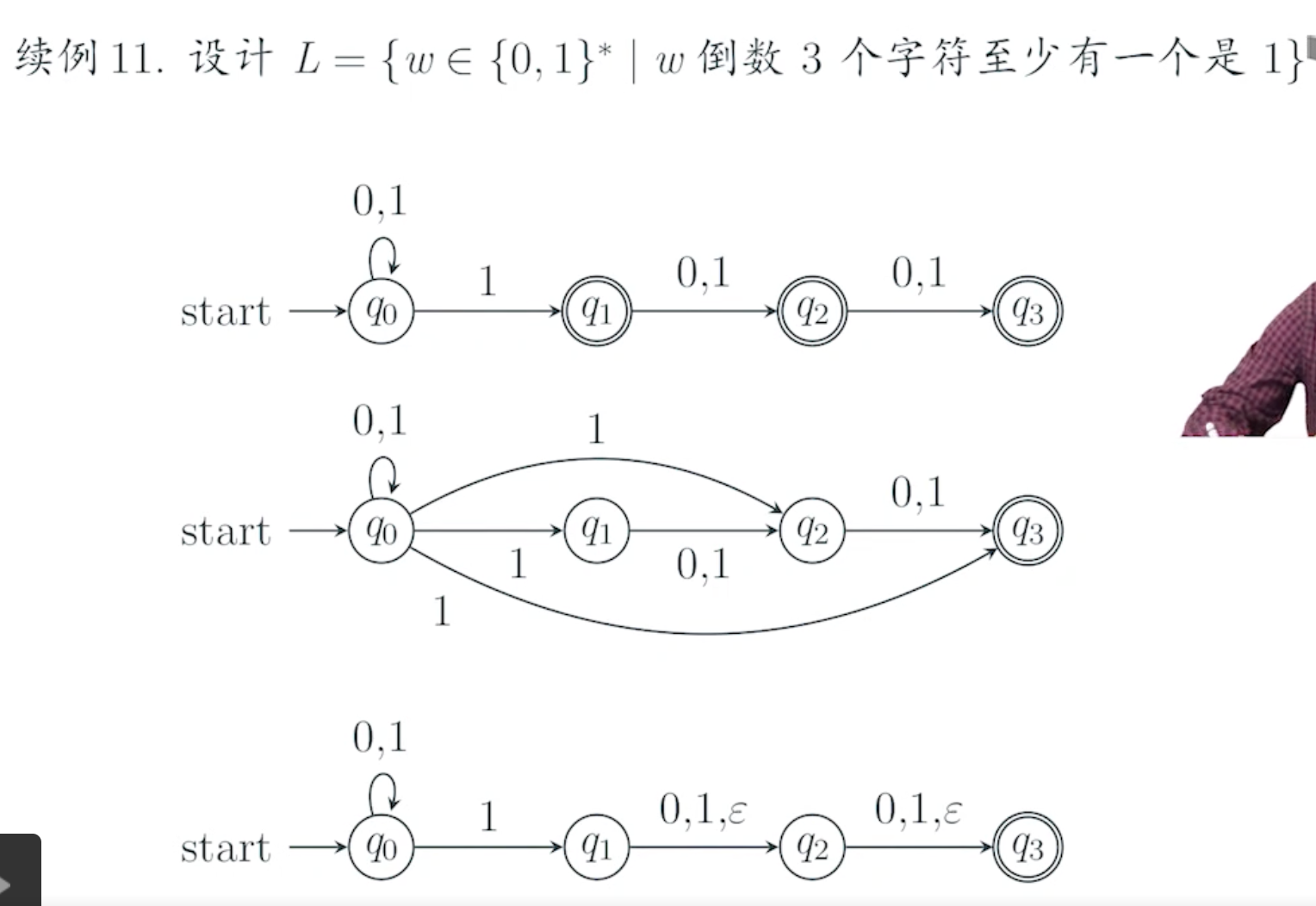
  最下面的 NFA 是带空转移的，使得自动机设计更加简单。

形式定义

带空转移非确定有穷自动机（$\epsilon-NFA$） A 为五元组

$$A = (Q, \Sigma,\delta,q_0,F)$$

其中

• $Q$：有穷状态集
• $\Sigma$：有穷输入符号集或字母表
• $\delta$：$Q \times (\Sigma \cup \{\epsilon\}) \rightarrow 2^Q$ 状态转移函数（因变量不再是特定状态，而是状态的集合，体现非确定性）
• $q_0 \in Q$：初始状态
• $F \in Q$​​：终结状态集或接受状态集

$\epsilon$​-NFA, NFA, DFA 之间的主要区别

• *自动机在某状态，读入某个字符时，可能有多个转移：*NFA， $\epsilon$-NFA
• *自动机在某状态，读入某个字符时，可能没有转移：*NFA, $\epsilon$-NFA, DFA
• 自动机在某状态，可能不读入字符，就进行转移：$\epsilon$​-NFA

注意：此后，不再明确区分 $\epsilon$-NFA和 NFA，而认为它们都是 NFA

闭包

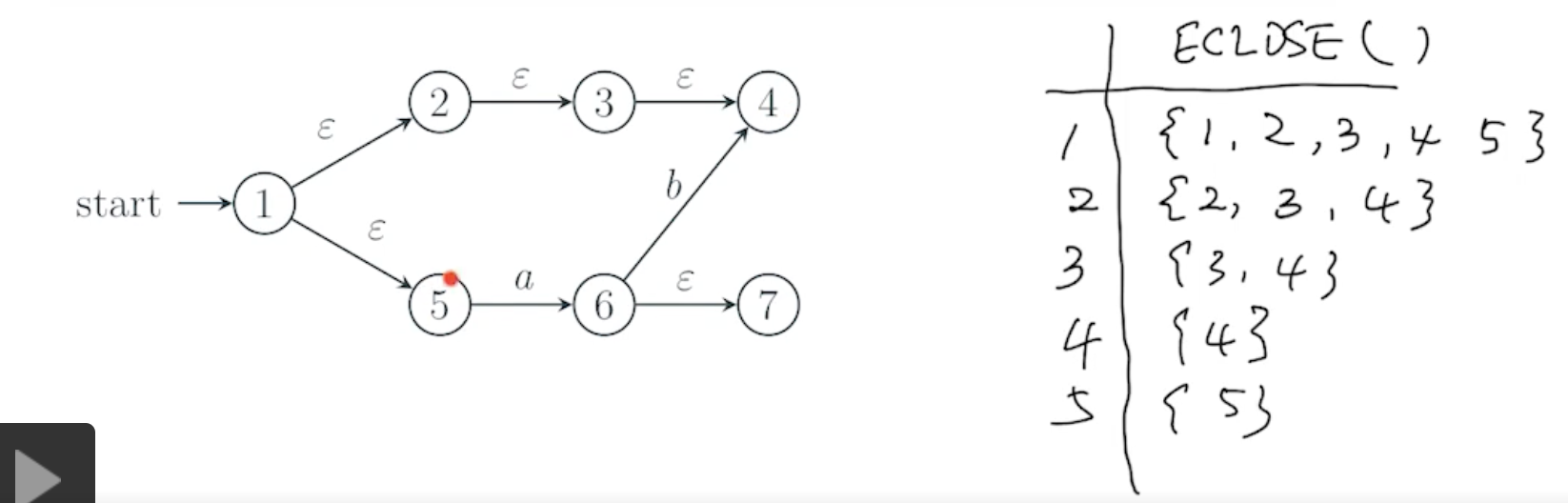
闭包的例子：

状态的 $\epsilon$ 闭包定义

状态 $q$ 的 $\epsilon$-闭包（$\epsilon-Closure$），记为 $\bold ECLOSE(q)$，表示从 $q$ 经过 $\epsilon \epsilon ... \epsilon$ 序列可达的全部状态的集合，递归定义为：

1. & q \in \bold ECLOSE(q); \\ 2. &\forall p \in \bold ECLOSE(q), 若 r \in \delta(p, \epsilon), 则 r \in \bold ECLOSE(q).

例子：

状态集合的 $\epsilon$-闭包定义

状态集 $S$ 的 $\epsilon$-闭包为

$$\bold ECLOSE(S) = \bigcup_{q\in S} \bold ECLOSE(q)$$

即状态集的闭包为状态集中每个状态的闭包的并集

扩展转移函数、语言、与 DFA 的等价性

阔转转移函数定义

扩展 $\delta$ 到字符串，定义扩展转移函数 $\hat \delta: Q \times \Sigma^* \rightarrow 2^Q$ 为

$$\hat \delta(q,w)= \begin{cases} \bold ECLOSE(q), & w = \epsilon \\ \bold ECLOSE(\bigcup_{p \in \hat \delta(q,x)}\delta(p,q)), & w=xa \end{cases}$$

其中 $a \in \Sigma, w,x \in \Sigma^*$.

即若字符串为空串，则当前状态转移到当前状态的闭包；若字符串不为空串，则当前状态转移到字符串对应状态的闭包。

$\epsilon$-NFA 的语言

与 NFA 一致，其语言的定义为：

若 $E = (q,\Sigma,\delta,q_0,F)$ 是一个 $\epsilon$-NFA，则 $E$ 接受的语言为

$$\bold L(E) = \{w \in \Sigma^* \mid \hat \delta(q_0, w) \cap F \neq \empty \}$$

与 DFA 的等价性的证明

==子集构造法==

==定理2==

第三章：正则表达式

正则表达式

正则表达式形式定义

几个特殊集合的运算

正则表达式的递归定义：

如果 $\Sigma$ 为字母表，则 $\Sigma$ 上的正则表达式递归定义为：

1. $\emptyset$ 是一个正则表达式，表示空语言

2. $\bold \epsilon$ 是一个正则表达式，表示语言 $\{\epsilon\}$

3. $\forall a \in \Sigma$，$\bold a$ 是一个正则表达式，表示语言 $\{a\}$

4. 如果正则表达式 $\bold r$ 和 $\bold s$ 分别表示语言 $R$ 和 $S$，那么

   $$\bold r + \bold s, \bold r \bold s, \bold r^*, (r)$$

   都是正则表达式，分别表示语言

   $$R \cup S, R \cdot S, R^*, R$$

正则表达式中三种运算以及括号的优先级（从上到下）

1. 括号
3. $\cdot$

正则表达式设计举例

自动机和正则表达式

DFA 到正则表达式之递归式法

定理 3：若 $L = \bold L(A)$ 是某 $DFA$ $A$ 的语言，那么存在正则表达式 $R$ 满足 $L = \bold L(R)$

状态消除法、正则表达式到 $\epsilon$-NFA

状态消除法：

• 从 DFA 中逐个删除状态
• 用标记了正则表达式的新路径替换被删掉的路径
• 保持 “自动机” 等价

定理 4：正则表达式定义的语言，都可以被有穷自动机识别

由正则表达式构造 $\epsilon$-NFA

任何正则表达式 e，都存在与其等价的 $\epsilon$-NFA $A$，即 $\bold L(A) = \bold L(e)$，并且 $A$ 满足：

1. 仅有一个接受状态
2. 没有进入开始状态的边
3. 没有离开接受状态的边

正则表达式的代数定律

等价

含有变量的两个正则表达式，如果以任意语言替换其变量，二者所表示的语言仍然相同，则称这两个正则表达式等价。

代数定律

在等价的意义下，正则表达式满足一些代数定律

• 并运算（加法运算）
  • 结合律
  • 交换律
  • 幂等率
  • 单位元 $\emptyset$
• 连接运算
  • 结合律
  • 单位元 $\epsilon$
  • 零元 $\emptyset$
  • ==不满足交换律==
• 加法运算和连接运算满足左右分配律
• 闭包运算
  • $(L^*)^*=L^*$
  • $\emptyset ^*=\bold \epsilon$
  • $\epsilon ^* = \bold \epsilon$​
  • $L^* = L^+ + \epsilon$
  • $(\epsilon + L)^* = L^*$

检验两个表达式相等

要判断表达式 $E$ 和 $F$ 是否等价，其中变量为 $L_1, ..., L_n$：

1. 将变量替换为具体的字母表中的字母，得到正则表达式 $\bold r$ 和 $\bold s$，例如，替换 $L_i$ 为 $a$
2. 判断 $\bold L(\bold r)$ 是否等于 $\bold L(\bold s)$，如果相等，则 $E = F$，否则 $E \neq F$.

注意：这种方法==仅限于==判断正则表达式，否则可能会发生错误。

因为这种方法采用用特殊证明一般的手段，因为正则表达式具有一些特质使得这种方法可行，其他的不一定可行。

第四章：正则语言的性质

正则语言的泵引理

正则语言的封闭性

正则语言的判定性质与自动机的最小化